A Prime Interview Question

If you want to skip to the interactive bit click here!

Recently I came across this slight variation on what I assume is a fairly common interview question.

“Given a number N, which of the below algorithms most efficiently checks if N is a prime number.”

To avoid completely giving away all the secrets, I only want to discuss the first solution that was provided:

For i from 2 to sqrt(N) inclusive:
	if n % i == 0:
		return False
return True

Even as someone who has not worked on any programming interview questions recently, I would say most of this solution pretty quickly made sense to me. In fact, it’s really not that far from the brute force solution most programmers probably think of right away. But why are we stopping at the square root of N? For me, that wasn’t clear at all.

It only took a small amount of googling to confirm. Pretty quickly it became clear that this is an accepted way to solve this problem. Easy enough, case closed. This solution was more efficient than the other two proposed solutions because it was the only proposed solution that didn’t consider all of the values for i between 2 and N. End of blog post … right? Well if you’ll humor me I think this is actually a pretty interesting question that is worth diving into for two reasons.

1. Despite the fact that it might seem like another “brain teaser” style interview question. This question does not actually require you to memorize the “one simple trick”. It really only requires knowledge of the definitions of primes and square roots.
2. I think if you take the time to fully understand how programming questions like this one tick, you’re much more likely to remember the answer if it comes up in an interview down the line.

Below is an animation I made that helps to demonstrate why this solution works! Enter any number between 6 and 100 and click the buttons to see the number line, factors, and lime green line for the square root of N. Notice how the paths between factors always cross over the green line drawn by the square root of N. (Numbers with few factors are pretty boring, but numbers with lots of factors like 24, 36, etc are the most interesting!)

Note: This should work fine on mobile, but is a bit easier to see on a larger screen

The rest of this post is going to be a deep dive into proving it!

Define the Problem

First, let’s get some terminology straight. What is a prime number? Taking straight from the wikipedia article:

“A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers.” ¹

In programmer terms a “natural number” is a positive integer (int). So the numbers [0,1,2,3] and so on. Add to that the information that one is not a prime number (see footnote) and we now are one step closer to our solution already. We care about the set of whole numbers (non-decimal) that are positive and greater than 1. So [2,3,4 …]

Now onto the second part!

“….. that is not a product of two smaller natural numbers”

When we say “the product of” in math, we just mean the result of multiplication. So as a simple example: 3*4=12 we could say that twelve is a product of 3 and 4.

The way I was always told to think about primes I think is a bit more intuitive:

“A natural number that is only evenly divisible by 1 and itself” ²

When we say “evenly divisible” we mean that the division will result in a whole number, no fractions or decimal points left over. So going back to our example we can verify that 12 is not a prime by either statement.

1. 12 is a product of two smaller natural numbers 3 and 4. So it cannot be a prime.
2. 12 is evenly divisible by a number other than 1 or itself : 3 -> 12/3 = 4. So it cannot be a prime.

Translate to Code

First, let’s just try to translate exactly the second statement into code : “A natural number that is only evenly divisible by 1 and itself”. Let’s check all those numbers.

for i in range(2, N):
	N % i

First, remember that the range() function in python is inclusive on the starting side (in this case 2) and exclusive on the ending side (in this case N). Meaning this for loop is the same as writing this is any of the more C flavored languages:

for (int i; i++, i < N) {
	N % i;
}

Second, a refresher on the % or modulo operator. The % operator returns the remainder of the division of two numbers. For example if you open up a python REPL you get the following:

>>> 15 % 3
0
>>> 11 % 2
1
>>> 2 % 0
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ZeroDivisionError: integer division or modulo by zero

We care about numbers that are evenly divisible. Or put more technically, have no remainder. So we can update our code to say:

for i in range(2, N):
	N % i == 0

And based on the input we don’t just want to spit out the result for every number in the list, we want to ensure that this holds true for every number that we checked along the way. And remember that if this statement is True for even a single value we know that N is not prime. This type of logic is sometimes called “short circuiting”, because we don’t have to finish the rest of loop. We know based on what we have seen what the result we be, regardless of the rest of the numbers in the range. So we basically get to take a shortcut and save some work (foreshadowing). Neat! That would look like this:

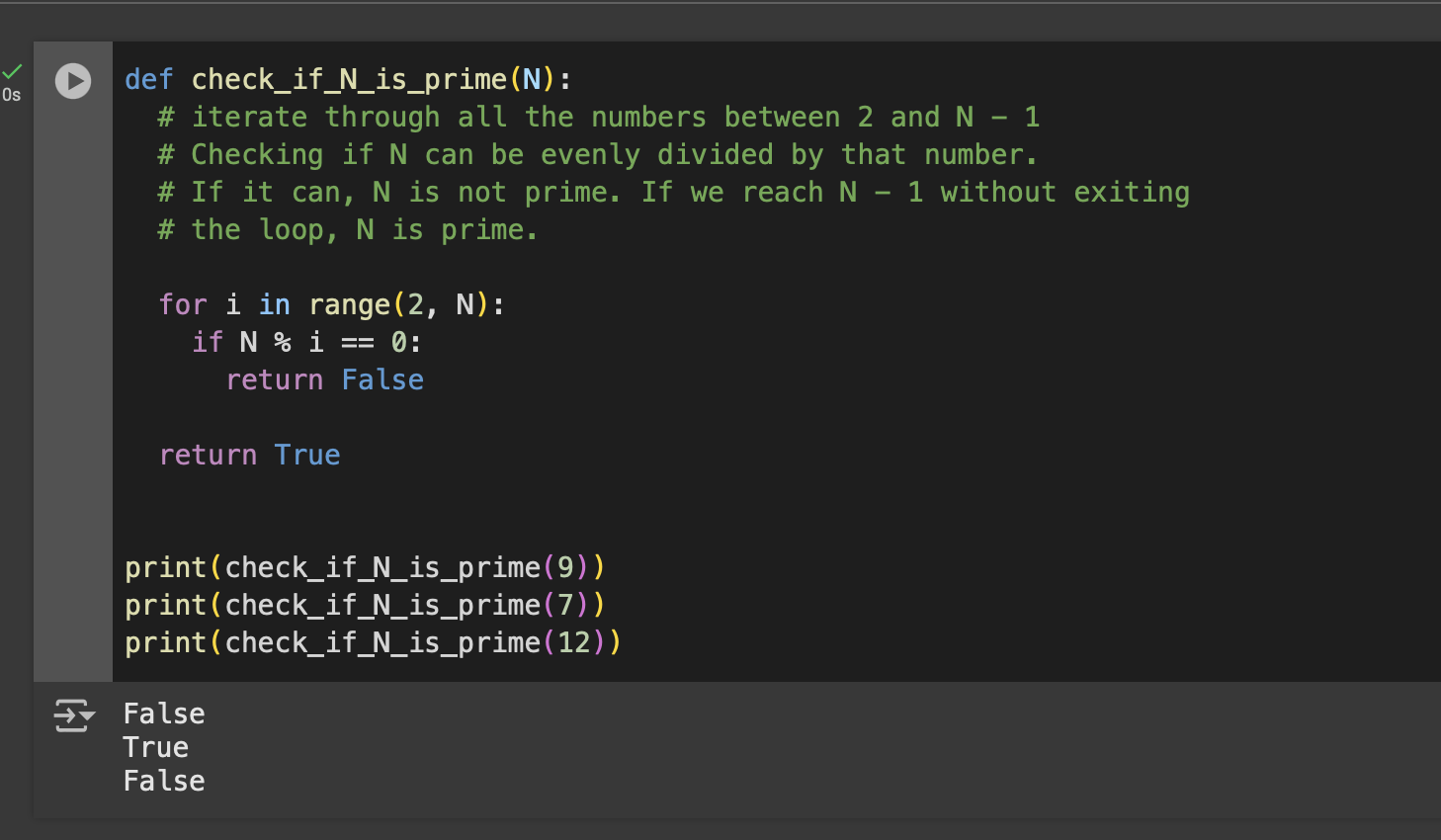
def check_if_N_is_prime(N):
	# iterate through all the numbers between 2 and N - 1
	# Checking if N can be evenly divided by that number.
	# If it can, N is not prime. If we reach N - 1 without exiting
	# the loop, N is prime.
	
	for i in range(2, N):
		if N % i == 0:
			return False
	
	return True
	

To get our short circuiting logic working correctly, we needed to add all of our logic into a function, but other than that nothing else has changed. And there you have it! this is a function that will check if a given number N is prime.

And now, finally, we can talk about that square root.

Optimization

First, let’s look at what exactly this code is doing.

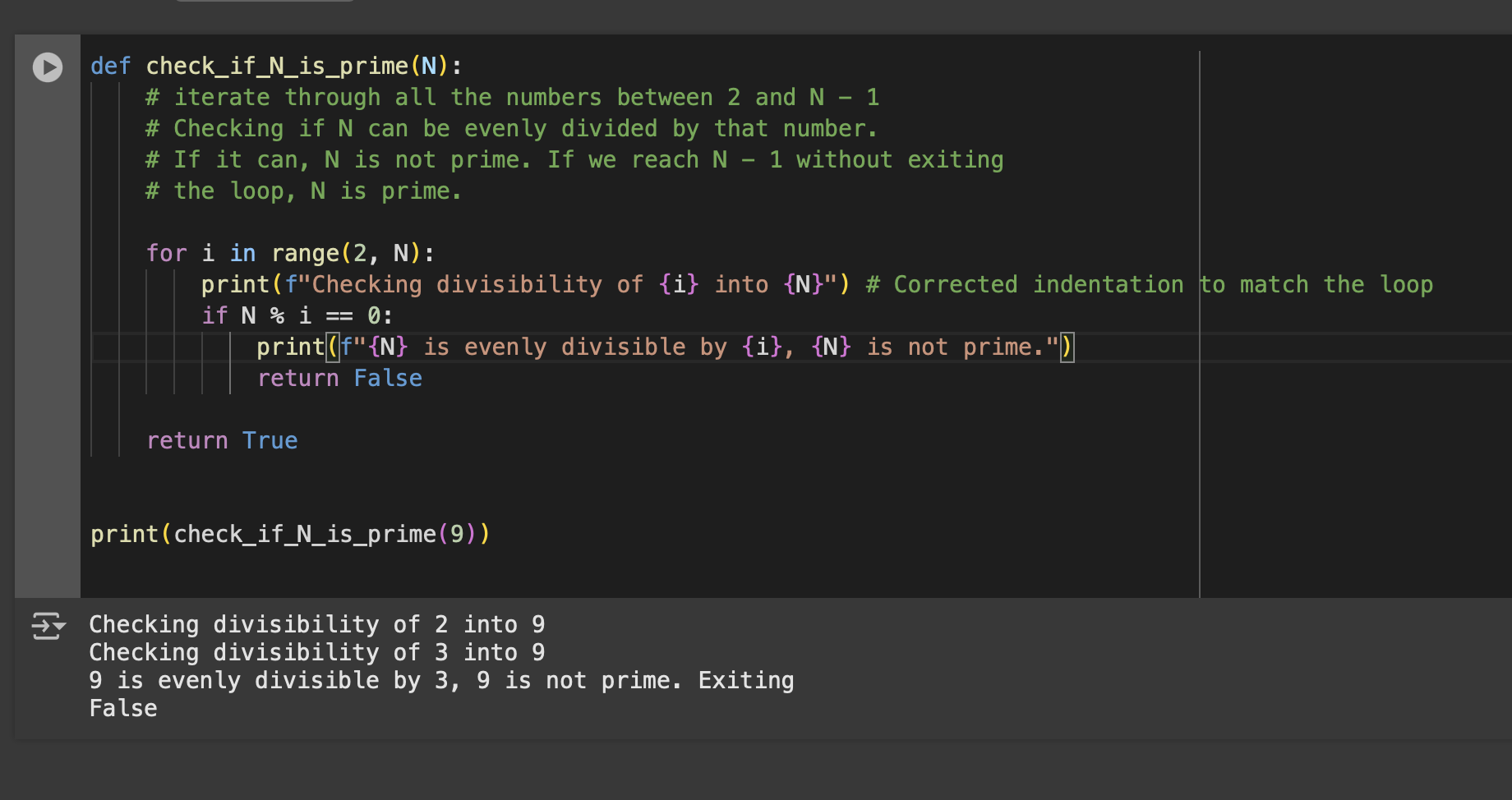
Here we can see the logical flow of the code properly short circuiting. Next let’s take a look at how it looks when N is prime.

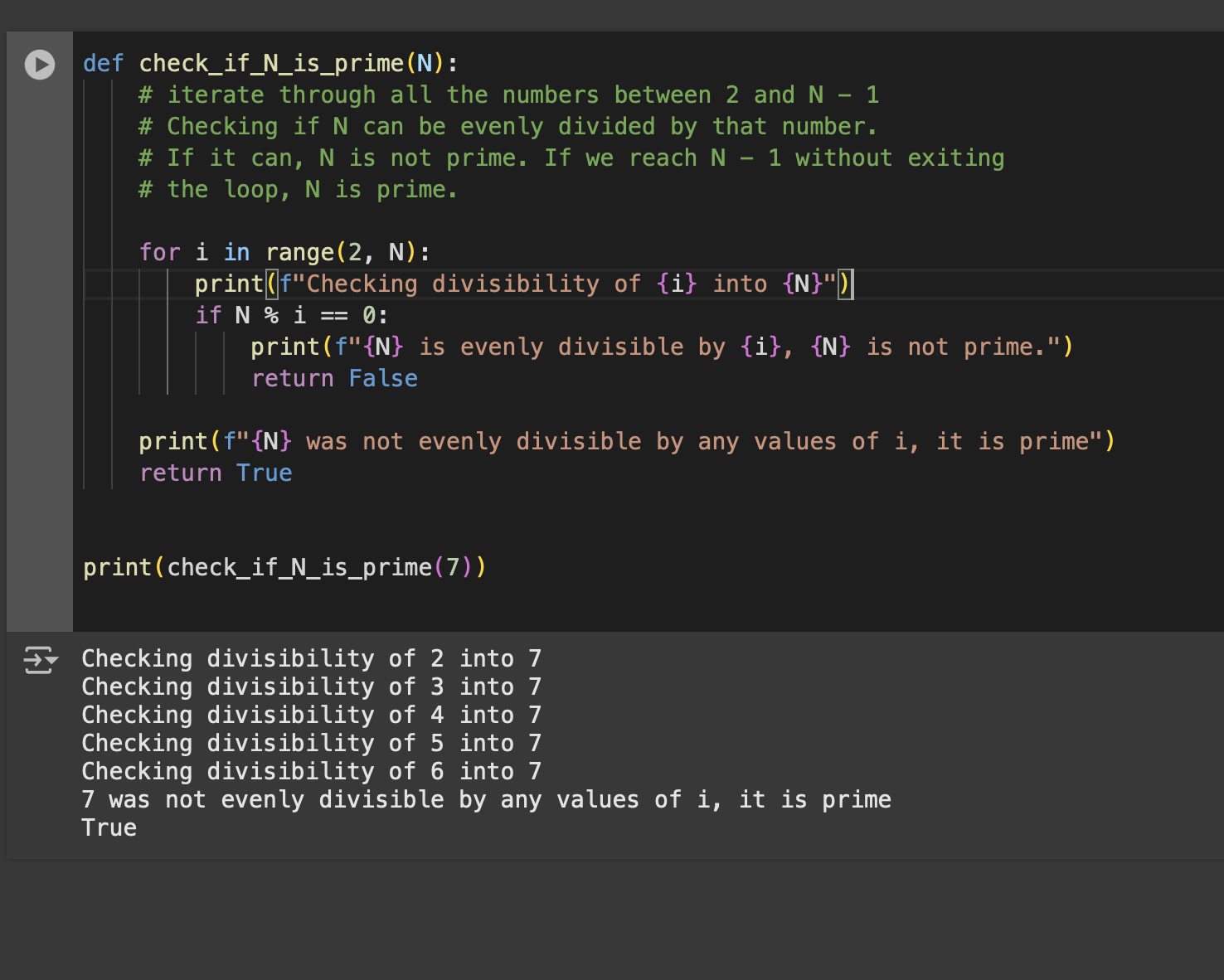
Seems like a lot of work just to find a prime, can we do better? Look at how much worse it is as the values of the prime get higher!

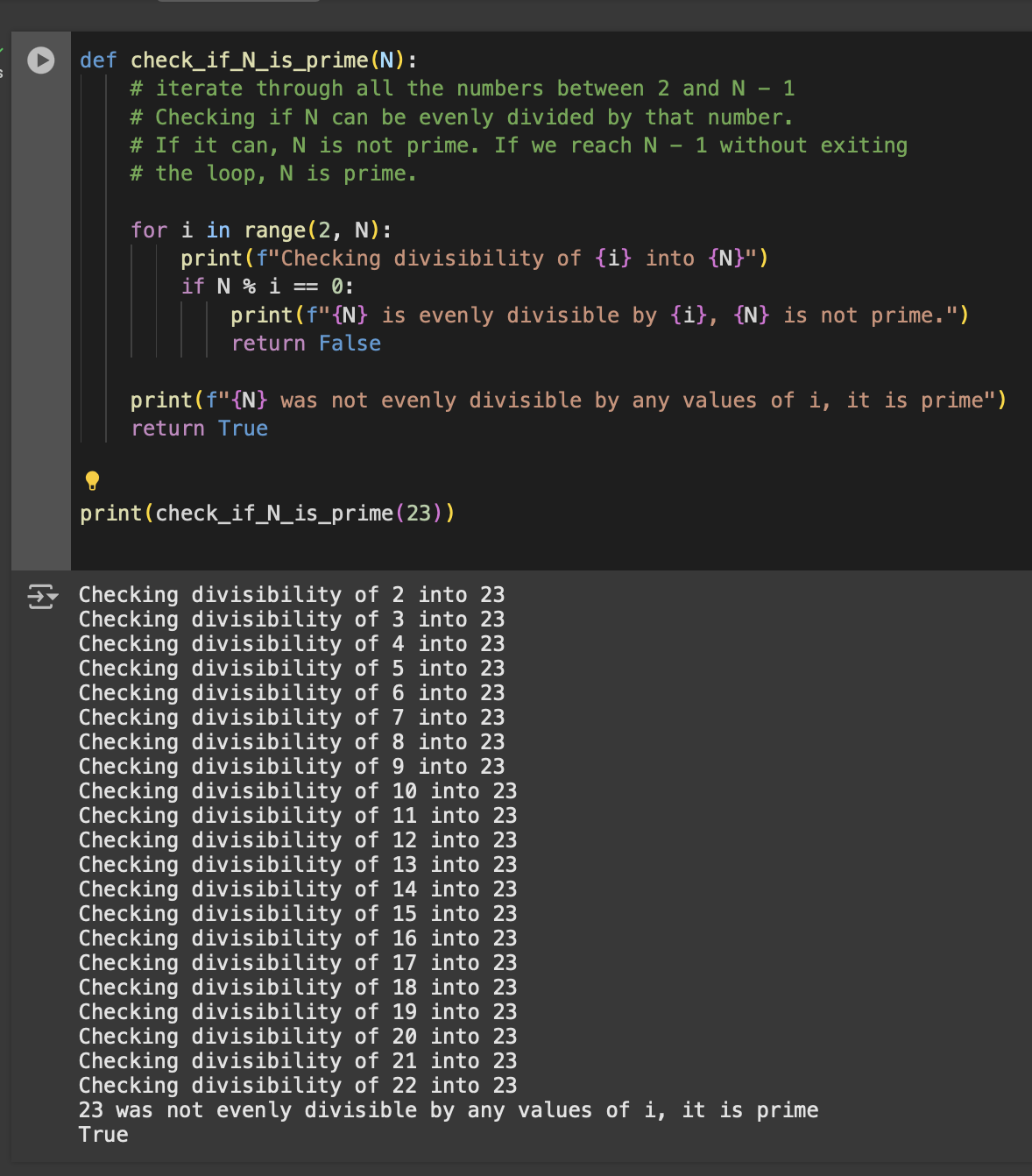
I actually had to zoom my browser window out a bit in google collab to fit all the output! But what we want to know is, is there a point in the loop where we can stop checking because we know that we’ve tried all possibilities? Can we do better than N - 1? Can we take advantage of that short circuiting logic for primes just like we did for non-primes? Let’s take a look at that first definition of prime again:

“A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers.”

If we once again think of those factors as a and b we can see that if we hold N constant (it’s the input of the problem) when we increase a, b must decrease. Writing down the factors for yourself, or plotting them on a number line and pairing them off can help clear this up.

N = 36
a x b = N

a = 2 -> 2 x 18 = 36

a = 3 -> 3 x 12 = 36

a = 4 -> 4 x 9 = 36

a = 5 -> 5 x 7.2 = 36

a = 6 -> 6 x 6 = 36

a = 7 -> 7 x ~5.153 = 36

a = 8 -> 8 x 4.5 = 36

a = 9 -> 9 x 4 = 36

Writing the factors out demonstrates the logic quite nicely. At the beginning, a < b with the value of b gradually decreasing until we reach a point where a = b and then after that we see that we continue to increase a and now a > b. But we’ve already tried all the whole number factors less than six! From this we know that when a = b , a is the maximum value that we have to check. After this peak value of b, we’re just going to be rechecking smaller values that we’ve already seen. This is driven home by the fact that when we get to a = 9 we’re just repeating the work we did at a = 4. With this in mind we can find the maximum value of a that we care about in terms of N.

a * b = N

when a = b

a * a = N

a^2 = N

a = sqrt(N)

Another helpful visualization is to pair off the factors for a given value of N on a number line. Starting with low values of a the corresponding value for b will be very far away on the number line, but as you increase that value more and more the values get closer and closer together until finally you reach the square root. After the square root you will find that you’re always pairing factors with numbers that are on the left, or smaller side of the square root. In this way the square root creates a dividing line between the smaller factors and the larger factors. All of the factors on the left side of the line must have a partner on the right side of the line and in turn all of the factors on the right side of the line have a partner on the left.

The interactive animation from the beginning of the article demonstrates this. In fact an example like that one is how I first came up with the idea to make it!

If you want to jump back to the animation click here!

Or look at it like a proof challenge you might have been given in high school. To prove that at least one of either a or b must be less than sqrt(N) is to imagine a situation where they are not:

a x b = N (from statement of the problem)

a > sqrt(N) (for the sake of argument)

b > sqrt(N) (we are in magic dream land)

therefore …

a x b > sqrt(N) * sqrt(N) (multiplication)

a x b > N (Cannot be the case! We said in line 1 that they are equal!)

So finally we can implement the correct solution.

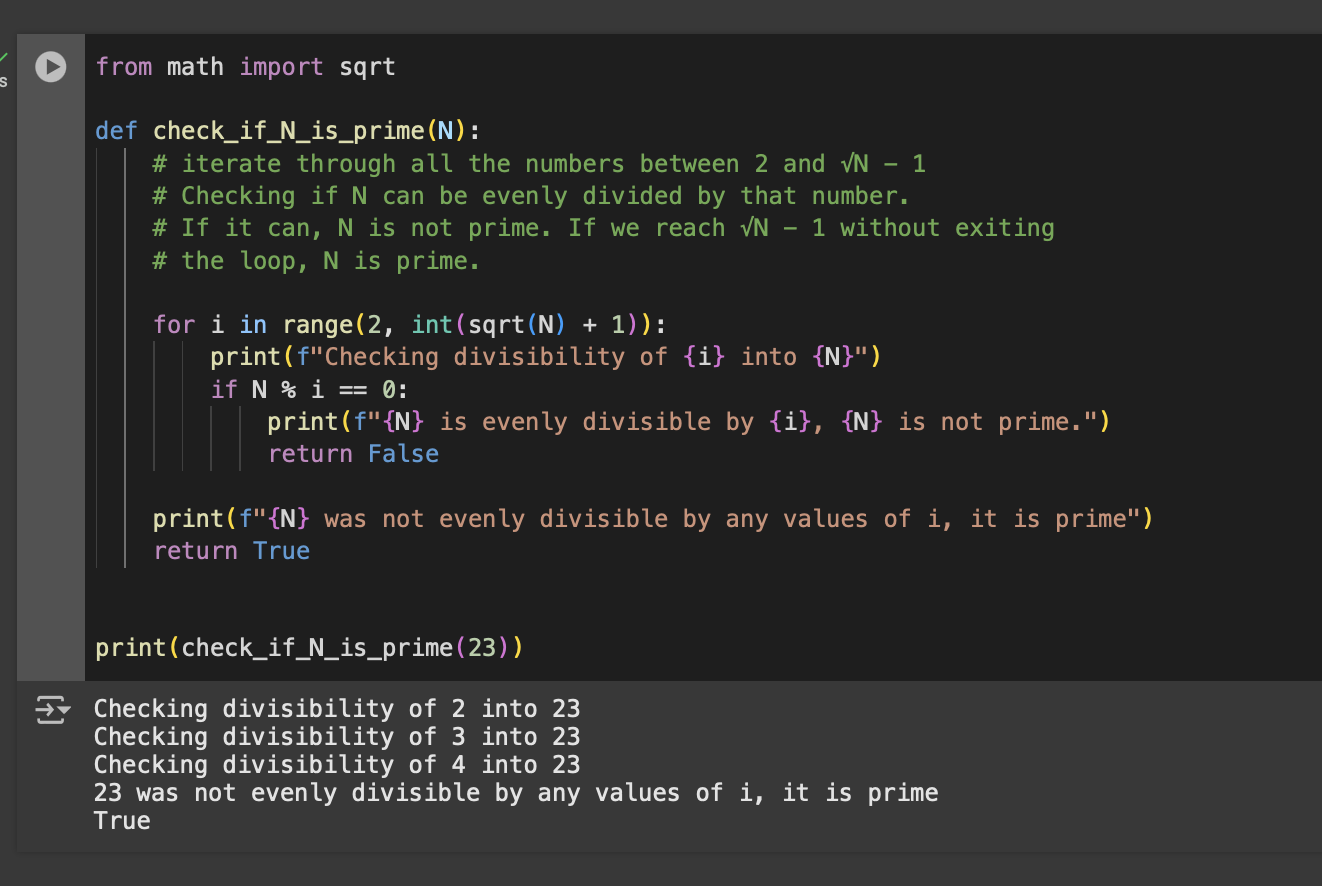
That sure was a lot of work just for O(sqrt(n)). But I hope you enjoyed that explanation as much as I did writing it! And I trust you’d be ready to knock that interview question out of the park next time it comes up.

Additional Reading and Links

Khan Academy Trial Division

Wikipedia Article on Trial Division Method

Wikipedia Article on Primes

Wikipedia Article on Modulo division

Wikipedia Article on Short circuit Evaluatiton

Footnotes: